Aleph Zero Home

Sometimes it is useful to specify a complex number by giving its distance from the origin, r and the angle θ that the red line makes with the horizontal axis. Then
z = re^iθ
This is called the polar form.

Suppose z = a + bi is a complex number. Then

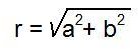
which is called the modulus of z, and is written |z|.

θ is the angle whose cosine is a / r. θ is called the argument of z and written arg(z).

To convert to polar form we have

• r = |z|
• θ = arccos(a/r)

To convert back

• a = r*cos(θ)
• b = r*sin(θ)
• z = a + bi

If z = a + bi then we can see from the above that
z = a + bi = r*cos(θ) + r*sin(θ)*i = r{cos(θ) + sin(θ)*i}
But {cos(θ) + sin(θ)*i} = e^iθ.

So z = re^iθ

Next Powers