Aleph Zero Home

We have seen how to add complex numbers. We can do subtraction in a similar way, treating the real and imaginary parts separately.
(a + bi) – (c + di) = (a - c) + (b - d)i

We have also seen how to multiply two complex numbers. So now we need to consider division.

If w and z are complex numbers we can write
w/z = w * 1/z
so, to do division, we just need to be able to find the reciprocal, 1/z, of a complex number z.

Suppose z = a + bi. We want to calculate 1/(a + bi).
Multiply the top and bottom of the fraction by a - bi and we get

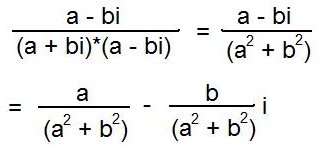
So now let us see what happens to Penny when we apply the mapping z |-> 1/z

->

Everything inside the unit circle maps to outside the circle. And everything outside the unit circle maps to inside the circle.

Applying the same mapping to the result will return everything to its original position.

Next Polar form