Quadratic Julia sets

Introduction - Julia Sets

Each point in the Mandelbrot Set is associated with a Julia set.

Remember the picture of the Mandelbrot set, coloured to show the limit periods.
This Julia set was generated using the point (0.25,0.55) which is in a purple bulb (period 4) of the Mandelbrot set.
This set comes from a point outside the Mandelbrot Set. It is just a collection of disconnected points.

The Maths

Julia sets are calculated by applying a rule, in exactly the same way as described for the Mandelbrot set. However, technically, the Julia set is the boundary between the black (inside) area and the coloured outside. The inside plus boundary is called a filled-in Julia set.

It is easiest to visualize this process if we treat the drawing area as the complex plane. If you are not familiar with complex numbers you can visit a little tutorial here. But understanding of complex numbers is not strictly necessary to follow this walk among the Julia sets. You can just imagine that the rules are applied to points rather than complex numbers.

The type of Julia set that you will most often see, is generated from the simple rule
newZ = Z * Z + C
where C is a fixed point.

I have it on good authority [1] that any quadratic polynomial, αZ² + βZ + γ where α, β and γ are constants, can be cast in the form Z² + C using a transformation which preserves the structure of the set. So I have not provided facilities in the Julia Set Explorer for the values of α and β to be input. So α=1 β=0 and γ=C.

The Mandelbrot set as an index to the Julia sets

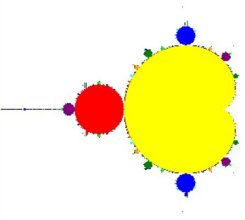
The structure of a Julia set depends on where C is, relative to the Mandelbrot set. If C falls inside the Mandelbrot set, then the limit set period of that part of the Mandelbrot set determines the general structure of the Julia set.

Here is a picture of the Mandelbrot set, coloured according to the period of the limit set. List of colours used
This is the Julia set for C= (-0.20833 , 0.765) which is in the blue bulb at the top of the Mandelbrot set, limit set period 3.
This is the Julia set for C= (-0.76667,-0.1) which is not in the Mandelbrot set. It is just a collection of disconnected points.

Colours of the limit set periods in the Mandelbrot Set

Period	Period	Period
1	2	3
4	5	6
7	8	9
10	11	12

Settings

Plot button	Draws the picture.
Input the point C	A point can be selected by tapping on the picture of the Mandelbrot set, or by entering the coordinates in the boxes.

Input X and Y	A point can be selected by tapping on the picture, or by entering the X and Y coordinates in the boxes.
Center on (X,Y) button	Sets the center of the picture. Useful when zooming in to see more detail.
Zoom In button	Magnifies the picture keeping the center fixed.
Zoom Out button	Keeps the center fixed as the contents of the picture shrink.
Reset button	Resets the center and zoom values.

Advanced settings
Maximum iterations : More iterations means a more accurate picture but the calculations will take longer.

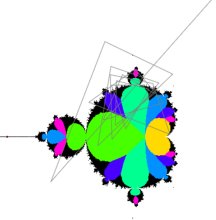
Here are a couple of images of the Julia set with C = (0,0.65). C is just outside the Mandelbrot set, so there should be no black areas. The Orbit Period Exploerer or The Limit Set Period Explorer can be used to check whether or not a point is inside the Mandelbrot set.

The set with C= (0,0.65) calculated to 100 iterations, showing black areas where insufficient iterations have been calculated.
The same set calculated to 1,000,000 iterations.
The orbit explorer shows that the point (0,0.65) is not in the Mandelbrot set.

1. Kenneth Falconer (2003) Fractal Geometry, Second Edition Wiley page 223