Cubic Mandelbrot and Julia sets

Introduction - Cubic Mandelbrot and Julia Sets

Overview

I have included this topic, Cubic Mandelbrot and Julia Sets, for those people who would like a bit more technical detail, and even some maths. If you just want to explore pretty patterns, you would do better sticking to the quadratic Julia sets.

The cubic polynomial that I have chosen to use is
Z³ – 3K²Z
where K is a constant, real or complex. According to Rucker [2], any cubic polynomial can be put into this form by changing the origin and coordinate system. So we do not lose any structure by restricting ourselves to this polynomial. See the Maths section for details of why I have chosen this form.

Instructions

The explorer shows two pictures. On the left is the cubic Mandelbrot set, and on the right the Julia set.

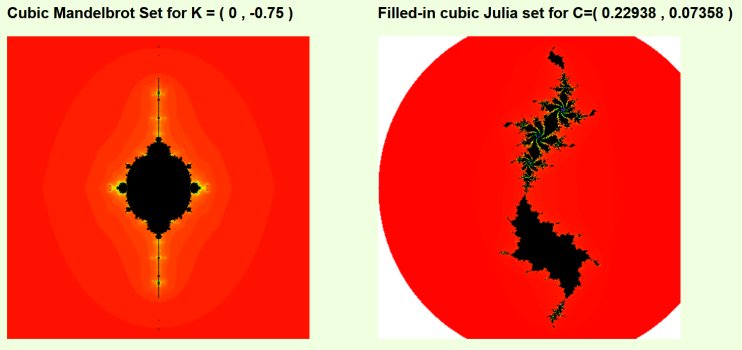
First choose your Mandelbrot set by entering values for K, and plot the set. Then click on a point in the Mandelbrot set to choose a value for C, and then plot the Julia set for these values of K and C.

Controls

Show Regions	Regions that are in the set for both critical points are shown in black and the regions that are in the set for only one of the critical points are shown in dark red and dark blue.
Show Periods	Show the limit set periods. This uses the same colours that were used for the quadratic Mandelbrot set.

When showing both Regions and Periods, the colours are greyed in regions that are in the set for only one critical point.

Zoom In Buttons	Zooms in keeping the center fixed
Zoom Out Buttons	Keeps the center fixed while shrinking the picture.
Center Buttons	Centres the picture on a point. The point is C for the Mandelbrot set, and P for the Julia set. Both C and P can be set either by clicking on the picture, or by entering the numbers in the boxes.

Advanced Settings

Mandelbrot iterations	The maximum number of iterations (maximum length of the orbits) when calculating the Mandelbrot set. A higher number means a more accurate picture, but takes longer to calculate.
Julia iterations	The maximum number of iterations when calculating the Julia set.
Zoom factor	The percentage increase or decrease in size for the Zoom buttons

The Maths

Julia sets can be created for any polynomial, or indeed, according to Falconer [1], any function that is analytic except, perhaps, at isolated poles. However, drawing the Mandelbrot sets is a bit more tricky. The iteration for each point has to start at a critical point of the function, and there may be more than one critical point. The critical points are at the zeros of the derivative.

A cubic polynomial will normally have two critical points. We have the polynomial
Z³ – 3K²Z, so the derivative is
3Z² – 3K². And this will be zero when Z = +K or -K.

To calculate the Mandelbrot set, for each point P, we iterate the function f(Z)=Z³-3K²Z+P

It is easiest to visualize this process if we treat the drawing area as the complex plane. If you are not familiar with complex numbers you can visit a little tutorial here. But understanding of complex numbers is not strictly necessary. You can just imagine that the rules are applied to points rather than complex numbers.

So for each point P in the picture we calculate two orbits, one starting with Z₀ = K, and one with Z₀ = -K.

Then the orbit for K goes like this.
Z₀ = K
Z₁ = f(Z₀) = f(K) = K³ – 3K³+P
Z₂ = f(Z₁) = f(-2K³+P) and so on.

If the orbit remains bounded the point P is in the set, but if the orbit wanders off into the distance then P is not in the set.

For some points the two orbits do not agree. If you make sure that the Show Regions box is checked before plotting the set, then the black area is where the two orbits agree. The dark blue and dark red areas show that only one of the orbits is bounded.

Even where both orbits are bounded, the two might lead to limit sets with different periods. When you plot the limit set periods, I have coloured the points according to the higher period. The Periods button will display the periods for the point C.

The Mandelbrot set as an index to the Julia sets

This Mandelbrot set is the same as that for the polynomial Z³+Z except for rounding when calculating √3.
Here is detail of the center of the set. The coloured blobs have limit set period 1 as well as the number indicated by the colour.
Here is the Filled-in Julia set with the point C in one of the coloured blobs. The blob has limit set periods 1 and 15.

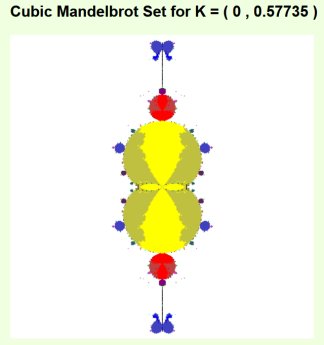
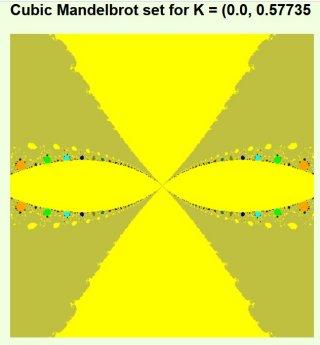
It seems to me, that the Julia set above has period 15 attributes, where 15 pieces join at a point alternating with bits that look more like the Julia set where both orbits have limit set periods of 1.

It also seems to me that point C for which both orbits are bounded leads to a Julia set which is connected.
With only one orbit bounded the Julia set is in a number of separate pieces.
And if neither orbit is bounded the Julia set is totally disconnected.

If I have got this wrong, or indeed made other mistakes, you can contact me on Facebook

Colours of the limit set periods in the Mandelbrot Set

Period	Period	Period
1	2	3
4	5	6
7	8	9
10	11	12

1. Kenneth Falconer (2003) Fractal Geometry, Second Edition Wiley page 215

2. Rudy Rucker (2010) Julia, Mandelbrot and ---- Rudy? https://www.rudyrucker.com/software/cubicmandel.htm